10.ケプラーの法則
| [目的] | 水星の軌道を作図し、ケプラーの3法則を理解する。 |
| [準備] | 分度器 三角定規 ものさし コンパス 方眼紙 |
| [操作] | 観測のデータを利用して軌道を作図し、ケプラーの3法則が成り立つことを確認する。 |
| [留意点・工夫点] | |
| ○ | 地球の公転軌道は離心率が非常に小さい(0.0167)ので、地球の公転軌道を円として表し、その中心を太陽とする。(地球の軌道の半径を半径5cmの円とすると作図しやすい) |
| ○ | 作図した線に内接するようになめらかな曲線で結ぶ(公転軌道)。この時、凹凸になったり、多角形になったりしないように注意する。 |
| ○ | 水星や金星のような内惑星は最大離角のデータで、火星のような外惑星の場合は、衝(地球から見て太陽と反対の方向にきた時)の日のデータで軌道を作図してもよい。 |
| ○ | 第二法則(面積速度一定の法則)を確認するとき、各観測点から隣の観測点まで移動したときにできる扇形の面積を測定し、それを移動に要した日数で割れば1日当たりの面積速度を求めることができる。この扇形の面積を求めるには、方眼紙のマス目を数えるとよい。 |
| ケプラーの法則 | |||
| プトレマイオス(ギリシア)が、すべての天体は地球を中心に運行するという天動説を唱えてから1000年以上たった16世紀に、コペルニクス(ポーランド)は、地球も他の惑星も太陽を中心とした円軌道を運行すると考えて惑星の運動を説明し、地動説を唱えた(1543)。 ティコ・ブラーエ(デンマーク)は、望遠鏡のなかった時代に、精密な天体観測を20数年間行った。彼の死後、助手のケプラー(ドイツ)が、観測資料の整理を続けた結果、地球も惑星も太陽を中心に運行し、だ円軌道を運行すると考えるとうまく説明できることに気づき、惑星の運動を3つの法則にまとめた(1609、1619)。これをケプラーの法則といい、ニュートンの万有引力の法則や運動の法則の発見の基礎となった。 |
|||
 |
|||
| 第一法則(だ円軌道の法則) | |||
| 惑星は、太陽を1つの焦点とするだ円軌道を公転する。 | |||
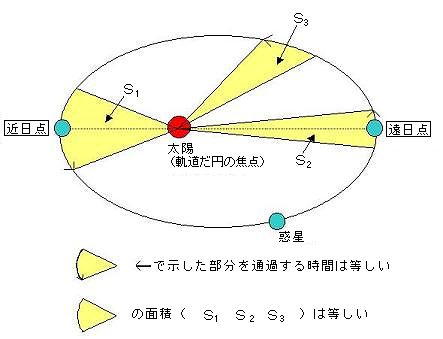
| 第二法則(面積速度一定の法則) | |||
| 惑星と太陽を結ぶ線分が一定時間に通過する面積は一定である。 | |||
| 第三法則(調和の法則) | |||
| 惑星の公転周期Tの2乗は、惑星の太陽からの平均距離(だ円軌道の半長軸)aの3乗に比例する。 | |||
| T2=ka3 (k:比例定数) | |||