| 学校名 |
伊丹市立西中学校 |
| 教科(科目等) |
数学 |
学年 |
3年 |
| 単元名 |
方程式 |
| 指導計画 |
本時 7/10
第一次 関数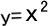 ・・・1時間 ・・・1時間
第二次 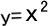 のグラフ ・・・2時間 のグラフ ・・・2時間
第三次 xとyの変域 ・・・2時間
第四次 変化の割合 ・・・2時間
第五次 関数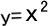 の利用 ・・・3時間 の利用 ・・・3時間 |
| 本時のねらい |
変化の割合の定義から、変化の割合がグラフ上で何を表しているのかを理解させる。 |
| 活用したICT機器 |
PC プロジェクタ |
| コンテンツの準備 |
| 関数グラフ作成ソフトウェアGrapes(フリーソフトウェア)で作成したグラフのコンテンツ |
| 授業でのICT活用の目的(意図) |
| 関数グラフ作成ソフトウェアを用いて、「xがsからtまで増加したとき」のy=a x 2(2乗)の変化の割合が、グラフ上で何を表わしているのかを図示する。また、tをsに近づけることで、変化の割合の値がsにおける接線の傾きに近づくことを示し、微分の考え方につなげていく。 |
| ICTを活用した場面及び主な活用方法 |
□導入 □展開 ■まとめ
・ 変化の割合の意味と求め方について復習した後、変化の割合がグラフ上で何を表しているのかについてGrapesのコンテンツを用いて説明した。
|
| ICT機器を活用するメリット |
・ 「xがsからtまで増加したとき」の変化の割合について考えるとき、Grapesを用いて説明すると、直線のグラフを図示したままsとtの値を自由に変えられるので、変化の割合が直線の傾きになっていることをわかりやすく提示できる。
・直線のグラフを図示したまま、tをsに近づけることで、直線が放物線の接線になっていく様子を目で見ることができ、高校で学習する微分の考えにつなげることができる。 |
| 活用のポイント |
・グラフを図示する手間を大幅に削減できるので、多くの例を示すようにする。数値を変化させて、直線のグラフが変化していく様子を動画のように示す。
・x、yの増加量や公式を使って変化の割合を求める演習の場面など、パソコンを使って説明する必要のないときはプロジェクタの電源を切っておく。必要なときだけ使うことで、コンテンツを使ったときの説明をより印象づけることができる。
|
| 担当教科等でICT活用授業が効果的であると思われる単元及び指導内容について |
・各学年の関数分野(比例・反比例、一次関数、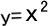 ) )
反比例のグラフで、x軸とy軸にグラフが近づいていく様子や、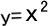 のグラフで原点付近も滑らかな曲線になっている様子などの図示 のグラフで原点付近も滑らかな曲線になっている様子などの図示
・1次関数のグラフで、傾きや切片を変化させたときのグラフの変化
・「放物線と直線の問題」や「グラフと図形の問題」などの応用 |